纤维缠绕成型是树脂基复合材料的主要制造工艺之一,是在控制张力和预定线型的条件下,将连续的纤维粗纱或布带浸渍树脂胶液、连续地缠绕在相应于制品内腔尺寸的芯模或内衬上,然后在室温或加热条件下使之固化制成一定形状制品的方法。
纤维缠绕技术的发展与增强材料、树脂体系的发展和工艺发明息息相关,尽管在汉代就有在长木杆外加纵向竹丝及环向蚕丝后浸渍大漆制造戈、戟等长兵器杆的工艺,但直到20世纪50年代纤维缠绕工艺才真正成为一种复合材料制造技术。1945年首次应用纤维缠绕技术成功制造了无弹簧的车轮悬挂装置,1947年第一台纤维缠绕机被发明。随着碳纤维、芳纶纤维等高性能纤维的开发和微机控制缠绕机的出现,纤维缠绕工艺作为一种机械化生产程度很高的复合材料制造技术,得到迅速的发展,20世纪60年代开始在几乎所有可能的领域都得到了应用。
第一节 概述
一、缠绕成型工艺的特点与分类
1.缠绕成型工艺的特点
缠绕成型工艺作为一种常用的复合材料成型方法,其特点包括:
(1)易于实现高比强度制品的成型。与其他成型工艺方法比较,以缠绕工艺成型的复合材料制品中纤维伸直和按规定方向排列的整齐和精确度较高,制品能充分发挥纤维的强度,因此比强度和比刚度均较高,如普通玻璃纤维增强复合材料的比强度即三倍于钢、四倍于钛。
(2)易于实现制品的等强度设计。由于缠绕时可以按照承力要求确定纤维排布的方向、层次和数量,因此易于实现等强度设计,制品结构合理。
(3)制造成本低,制品质量高度可重复。缠绕制品所用增强材料大多是连续纤维、无捻粗纱和无纬带等材料,无须纺织,从而减少了工序,降低了成本,同时也避免了布纹交织点与短切纤维末端的应力集中。纤维缠绕工艺容易实现机械化和自动化,产品质量高而稳定,生产率高,便于大批量生产。
(4)适于耐腐蚀管道、储罐和高压管道及容器的制造,这是其它工艺方法所不及的。
虽然目前缠绕成型工艺是各种复合材料成型工艺中机械化、自动化程度较高的一种,能制造出性能优良的制品,但是它也存在如下局限性:
(1)在湿法缠绕过程中易形成气泡,造成制品内孔隙过多,从而降低层间剪切强度、压缩强度和抗失稳能力。因此,要求在生产过程中尽量采用活性较强的稀释剂,控制胶液粘度,改善纤维的浸润性及适当增大纤维张力等措施,以便减少气泡和孔隙率。
(2)缠绕复合材料制品的开孔周围应力集中程度高,层间剪切强度低。为了连接配件而开口进行的切割、钻孔或开槽等都会降低缠绕结构的强度。因此要求结构设计合理,制品完全固化后尽量避免切割、钻孔等破坏性的加工。对于确需开孔、开槽的复合材料制品需要采用局部补强措施。
(3)对成型制品的形状有局限性,不太适宜于带凹曲线表面(双负曲率曲线)部件的制造。到目前为止,缠绕制品多为圆柱体、球体及某些正曲率回转体,如管、罐、椭圆运输罐等。对于非回转体或负曲率回转体制品的缠绕规律及缠绕设备比较复杂,尚处于研究阶段。
2.缠绕成型工艺的分类
纤维缠绕成型工艺按其工艺特点,通常分为三种:
(1)干法缠绕成型工艺 将连续的玻璃纤维粗纱浸渍树脂后,在一定的温度下烘干一定时间,除去溶剂,并使树脂胶液从A阶段转到B阶段,然后络纱制成纱锭,缠绕时将预浸纱带按给定的缠绕规律直接排布于芯模上的成型方法,称为干法缠绕成型工艺。
采用该法制成的制品质量比较稳定,缠绕速度可以提高(可达100~200m/min),工艺过程易控制,设备比较清洁,可以改善劳动卫生条件。这种工艺方法容易实现机械化、自动化。该工艺要求所使用的固化剂在纱带烘干时不应升华或挥发,特别是采用酸酐及DDS类等高温固化的树脂基体系统,常常易出现制品内层贫胶、外层富胶,有的表面有较多甚至较大的气泡,表面不光滑。并且由于纱片缠绕时每束已浸渍树脂胶的纤维束被张紧得犹如一条连续匀称的薄片需要预浸、烘干和络纱,因此,缠绕设备复杂,投资较大。
(2)湿法缠绕成型工艺 将连续玻璃纤维粗纱或玻璃布带浸渍树脂胶后,直接缠绕到芯模或内衬上而成型增强塑料制品,然后再经固化的成型方法称为湿法缠绕成型工艺。
湿法缠绕工艺设备比较简单,对原材料要求不严,便于可选用不同材料,因纱带浸胶后马上缠绕,对纱带的质量不易控制和检验,同时胶液中尚存大量的溶剂,固化时易产生气泡,缠绕过程中纤维的张力也不易控制。缠绕过程中的每个环节,如:浸胶辊、张力控制器、导丝头等,经常需要人进行维护,不断涮洗,使之保持良好的工作状态。万一某一环节发生纤维缠结,势必影响整个缠绕工艺及产品质量,有时会造成浪费。
(3)半干法缠绕成型工艺 这种工艺与湿法相比增加了烘干工序,与干法相比,缩短了烘干时间,降低了胶纱烘干程度,可在室温下进行缠绕。这种成型工艺既除去了溶剂、提高了缠绕速度,又减少了设备,提高了制品质量。
二、缠绕成型工艺的现状与发展
目前,缠绕制品在军、民两方面都有应用。军用产品的特点是高性能及精确的缠绕结构。民用主要产品有贮罐、管材和压力容器,尤其是现场缠绕技术的运用,解决了从前对纤维缠绕大型贮罐尺寸受限制的问题,大大拓宽了缠绕制品的使用范围,而夹砂纤维缠绕管线的投产则开辟了玻璃钢管在供水系统中的应用。
纤维缠绕可通过增强材料、基材及工艺结构的优选使制品性能达到最佳,是较为先进的玻璃钢成型工艺,但其目前仍有许多问题有待进一步研究和解决:
(1)在结构设计方面,缠绕工艺和结构设计的结合仍不够紧密,应进一步加强,通过结构设计所确定的合理的产品结构形式和设计参数来最后确定合理的工艺制度,以提高产品质量、生产效率和技术经济指标。
(2)在原材料方面,对材料性能的研究仍有待深入,如增强材料的强度,树脂的延伸率、耐高温、耐腐蚀性能及工艺性等。
(3)对自动化缠绕设备的研制还有待提高,以确保生产工艺过程的最大稳定性及制品的可靠性和耐久性,提高劳动生产率。
(4)由于原材料和工艺过程的变化对产品性能影响很大,因此还要对从原材料到产品的整个工艺中的各个环节进行检验和管理,建立健全和严格的质量检验和管理制度。
第二节 缠绕成型工艺原理
对缠绕成型工艺原理的分析,主要是研究缠绕规律,即导丝头与芯模之间相对运动的规律,以满足纤维均匀、稳定和规律地缠绕到芯模上。通过对缠绕规律的研究,可以找出制品的结构尺寸与线型以及导丝头与芯模相对运动之间的定量关系,从而确定具体产品的最佳缠绕工艺制度。
一、缠绕规律分类
无论何种形式的缠绕,都归结到三类中:环向缠绕、平面缠绕和螺旋缠绕。
(1)环向缠绕。环向缠绕是沿容器圆周方向进行的缠绕。缠绕时芯模绕自己轴线作匀速运动,导丝头在平行于芯模轴线方向的筒身区间运动。芯模每转一周,导丝头移动距离为一个纱片宽。如此循环下去,直至纱片均匀布满芯模圆筒段表面为止,如下图所示:
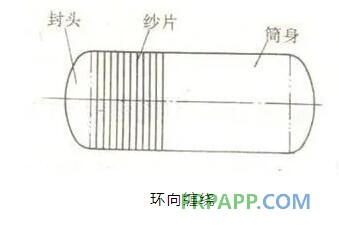

环向缠绕的特点是缠绕只能在筒身段进行,不能缠到封头上去。邻近纱片间相接而不重叠,纤维的缠绕角通常在85°~90°之间。为使纱片能一片挨一片地布满芯模表面,就必须保证芯模与导丝头的平移,保证两个运动的相互协调。
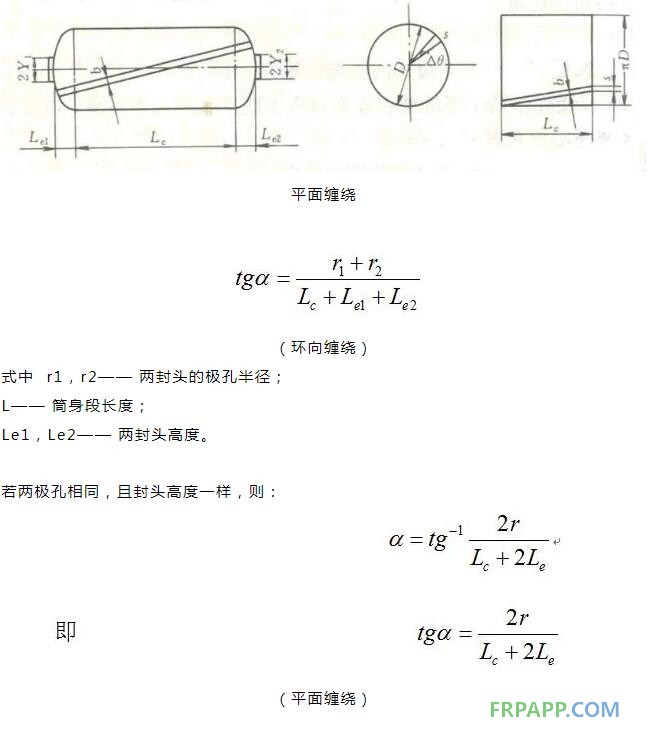
(2)平面缠绕。平面缠绕时,导丝头在固定平面内作匀速圆周运动,芯模绕自己轴线慢速旋转。导丝头每转一周,芯模转过一个微小角度,反映到芯模表面上是一个纱片宽度。纱片与芯模纵轴成0°~25°的交角,并与两端极孔相切,依次连续缠绕到芯模上去。纱片排布彼此不发生纤维交叉,纤维缠绕轨迹是一条单圆平面封闭曲线。
平面缠绕的速比是指单位时间内芯模转数与导丝头旋转的转数比,纱片与纵轴的交角称为缠绕角(α),如下图所示:
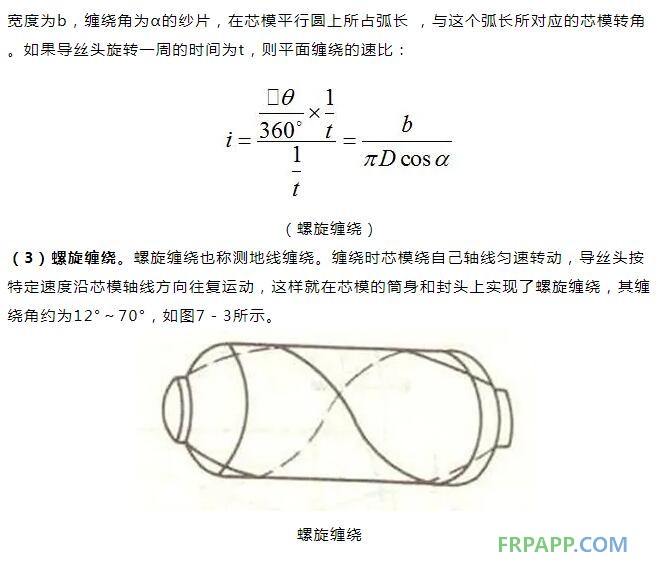


在螺旋缠绕中,纤维缠绕不仅在筒身段进行,而且在封头上也进行。其缠绕过程为:纤维从容器一端的极孔圆周上某一点出发,沿着封头曲面上与极孔圆相切的曲线绕过封头,并按螺旋线轨迹绕过圆筒段,进入另一端封头,然后再返回到圆筒段,最后绕回到开始缠绕的封头,如此循环下去,直至芯模表面均匀布满纤维为止。由此可见,螺旋缠绕的轨迹是由圆筒段的螺旋线和封头上与极孔相切的空间曲线所组成,即在缠绕过程中,纱片若以右旋螺纹缠到芯模上,返回时,则以左旋螺纹缠到芯模上。
螺旋缠绕的特点是每束纤维都对应极孔圆周上的一个切点;相同方向邻近纱片之间相接而不相交,不同方向的纤维则相交。这样,当纤维均匀缠满芯模表面时,就构成了双层纤维层。
二、螺旋缠绕规律分析
目前,对于缠绕规律的研究主要采用两种分析方法:标准线法和切点法。标准线法的基本点就是通过容器表面的某一特征线——“标准线”来研究制品的结构尺寸与导丝头、芯模相对运动规律。这种方法直观性强易学懂,但分析演算过程较为复杂,精确性也不太高。切点法是研究缠绕线型在极孔上对应切点的分布规律研究纤维缠绕芯模转角与线型、速比之间的关系。该方法的理论性较强数学推导比较严密。这两种分析方法的出发点虽不相同,但并无本质区别,下面就用这两种方法分析螺旋缠绕规律。
1. 名词解释
(1)标准线。螺旋缠绕时芯模绕其轴线转动,导丝头平行芯模的轴线作往复运动,由导丝头引出的纤维从芯模上某点开始,经过几次往复运动后,纤维又绕回到原始点,这样在芯模上完成了第一次铺纱,称为标准线。
标准线的排列形式不同,其线型不同,缠绕规律也不同,因此,标准线是反映缠绕规律的基本线型。下图为n=4,k=1时螺旋缠绕标准线展开图。
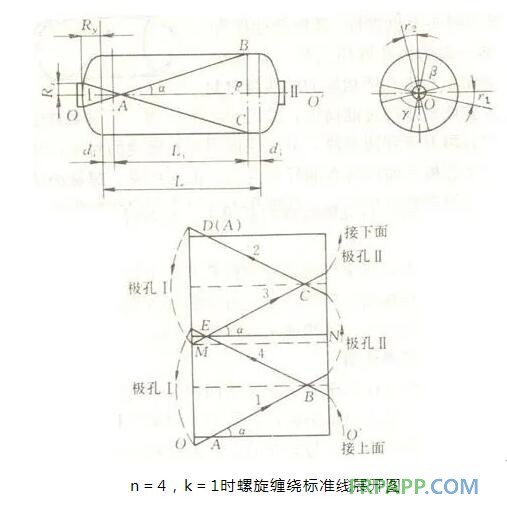

由图可知,纤维从A点开始缠绕,其走向是A→B→极孔Ⅱ→C→D(与A重合)→极孔Ⅰ→E→C→极孔Ⅱ→B→E→极孔Ⅱ→回到起始点A,这条布线我们叫做标准线。螺旋缠绕始终是沿某一标准线进行,区别仅在于每缠绕完一个标准线后,纤维应错过一个纱片宽度,按此进行下去,直至芯模表面布满纤维为止,此时,称为一个交叉缠绕循环,而显示在芯模上,则是两层交叉纤维。
(2)交叉点。在标准线上互不平行的缠绕纤维的交点称为交叉点。同一结构尺寸的容器,采用不同缠绕规律时,其交叉点数目和位置也不相同。图中A、B、C、D、(A)、E各点即为交叉点。
(3)交带。螺旋缠绕走过一个循环,由交叉点组成的迹线叫做交带。见图中A、E、D及B、C的连线即为交带。它是一条垂直于轴线的截圆线。而在筒身两端,距筒身与封头交线某距离处,各存在一条重合于交带的截面圆线,我们称这个截面圆线为基准线。
(4)常用符号
Lc——容器内衬的筒身长度;
D——内衬直径;
Rx——封头处极孔半径(封头曲线对x轴坐标值);
Ry——对应于值Rx值的y轴坐标值;
α——缠绕角,它表示纤维在芯模上的走向与芯轴轴线的夹角;
β——标准线在封头部的包角。它表示纤维自进入封头到绕出封头时,芯模所转过的角度;
γ——标准线在筒身段的进角。它纤维自筒身一端绕至另一端时,芯模转过的角度;
n——人为把圆筒体圆周等分数目;
Li——筒身两端基准线间的距离;
di——基准线至筒身和封头交界线间的距离;
J——平面缠绕循环数;
K——纵向纤维利用系数(K=0.7~0.8);
f——每束纤维的平均强度,79.8N/束;
Nθ,Nf——环向和平面缠绕纱片的纤维束数(束/条);
m,M——环向缠绕时纱片密度,条/cm;
P——容器内部压力,710-1MPa;
R——容器半径。
计算公式:


2. 用标准线法分析螺旋缠绕规律
任何线型的缠绕工艺,都要求芯模与导丝头作不同规律的相对运动,所以对缠绕规律的分析,就是要找出产品结构尺寸与缠绕参数,比如缠绕角、速比等之间的函数关系。下面以受内压圆筒形容器为例进行分析。
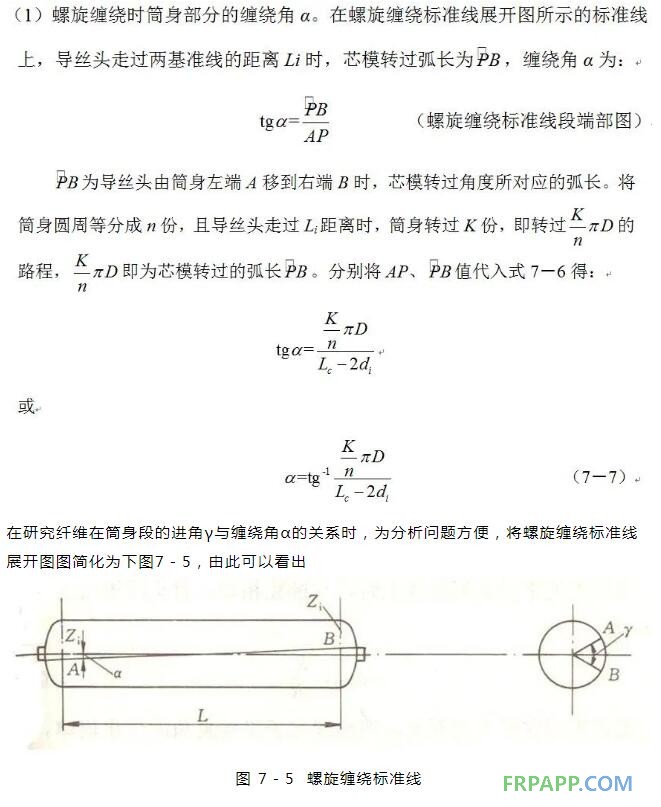


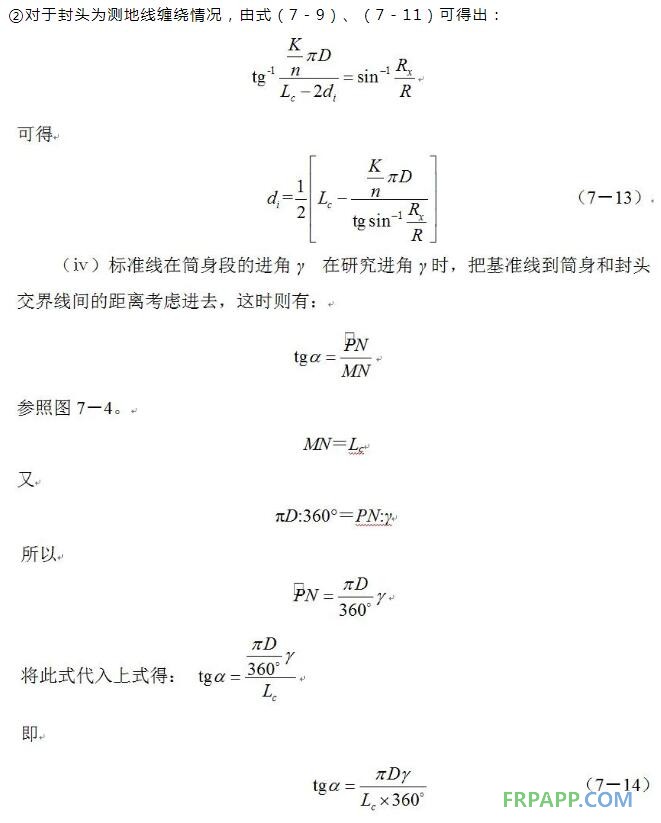
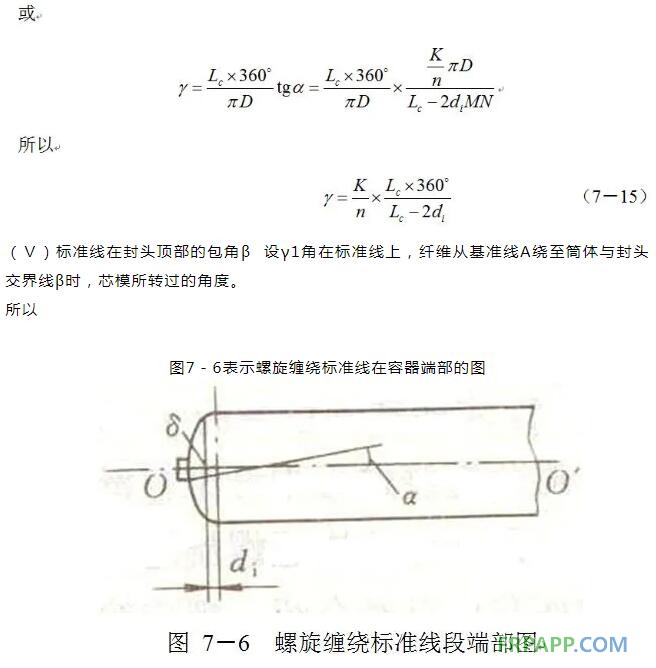









这些参数,同时还与容器尺寸、缠绕角α及基准线至筒身和封头交界线间的距离di有直接关系,只有全面考虑研究,才能选到恰当的n、K值,才能使选定的缠绕规律与容器相适应,避免缠绕过程中纤维打滑、偏斜等异常情形的发生。
3. 用切点法分析螺旋缠绕规律
前面我们已经介绍,螺旋缠绕是一种连续的纤维缠绕过程,缠绕纤维的轨迹是由筒身部分的螺旋线和封头部分与极孔相切的空间曲线组成。
螺旋缠绕的线型与切点的位置和数量有关,也就是说,与纤维在封头极孔圆周上切点位置有关。因此,对于纤维在芯模表面上分别规律的研究,可以通过研究切点在极孔圆周上的分布及分布规律解决。这就是用切点法描述螺旋缠绕规律的基本思想。
A. 线型
所谓线型,就是连续纤维缠绕在芯模表面上的排布型式。用切点法描述螺旋缠绕的线型时,主要是使线型与切点数和分布规律联系起来进行研究。
(1)纤维在芯模表面均匀布满的条件
(ⅰ)一个完整循环的概念。在芯模上联系缠绕的纤维,由导丝头引入从芯模上某点开始,导丝头经过若干次往返运动后,又缠回到原来的起始点上,这样的一次布线称为标准线。完成一个标准线缠绕或者说完成与初始切点重合的缠绕,称为一个完整循环。由此可以看出,要使纤维均匀缠满芯模表面,则需要若干条由连续缠绕纤维形成的标准线。换以言之,需要进行若干个完整循环缠绕才能实现。标准线的排布型式,即缠绕花纹特征包括切点、交叉点、交带及其分布规律。它反映了全部缠绕的花纹特征。因此,标准线是反映缠绕规律的基本线型。
(ⅱ)一个完整循环缠绕的切点数及分布规律
a.切点的时序相邻和位置相邻的概念。时序相邻:在极孔圆周上按时间顺序相继出现的两个切点。它们的相互位置只有两种情况。一是两切点之间密排而不再加入其他切点,称这两个切点为位置相邻;二是两切点之间还要加入其他切点,称这两切点位置不相邻。但它们均表明的是切点位置及其出现的顺序。
b.单切点与多切点。完成一个完整循环缠绕有两种情况:第一种情况与起始切点位置相邻的切点,时序上亦相邻,因此,在出现与起始切点位置相邻的切点之前,极孔圆周上只有一个切点,所以称为单切点。第二种情况,与起始切点位置相邻的点在时序上不相邻。也就是说,在出现与起始点位置相邻的切点以前,极孔圆周上已有两个以上切点,这种情况称之为多切点(切点数n=2、3、4……)。
由于芯模匀速转动,导丝头么每次往返时间又相同,所以在极孔圆周上的几个切点等分圆周。单切点与两切点的排布顺序如图7-7。
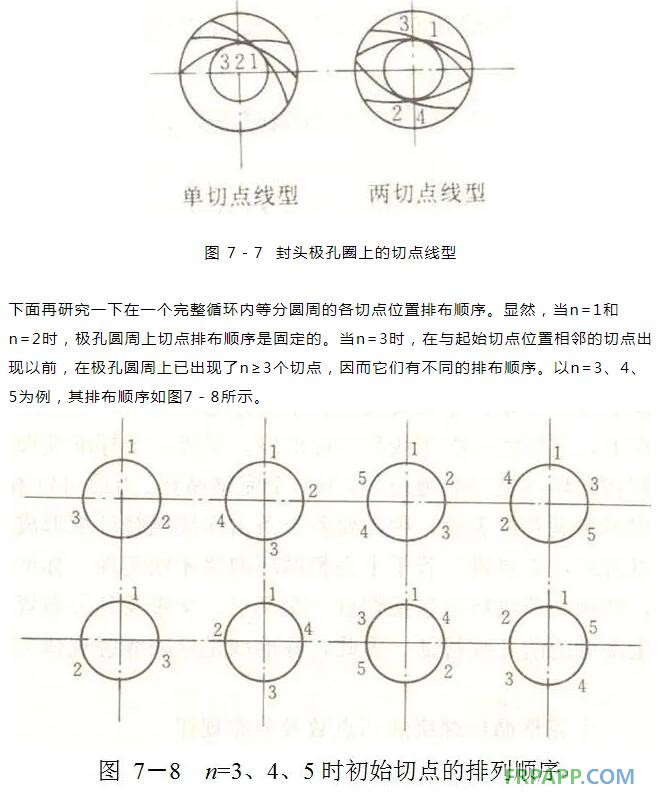

由此可以看出,不同的线型其切点数及各切点的排列顺序不同。
(ⅲ)纤维在芯模表面均匀布满的条件。由于芯模上的每一束纱片,都对应极孔圆周上的一个切点。因此,只要满足了下列条件,就可实现在经过若干完整循环缠绕后,纱片能一片换一片地均匀布满整个芯模表面。
①完成一个完整循环地诸切点等分芯模转过的角度,即诸切点均布在极孔圆周上。
②相邻的两切点所对应的纱片在筒身段错开的距离等于一个纱片宽度,显然,由于条件①,其他陆续缠绕经过对应切点的纱片,在筒身上错开的距离也等于一个纱片宽度。
于是,对于纤维缠绕均匀布满芯模表面的排布规律,就可以通过对一个完整循环缠绕纤维排布规律的研究来解决。而完成一个完整循环缠绕规律的线型,又可以通过诸切点在极孔圆周上的分布规律来分析。
下面我们找出能够满足以上这两个条件的芯模与导丝头的运动关系。
(2)纤维缠绕芯模转角即缠绕中心角与线型的关系。一个完整循环缠绕,即出现与起始切点位置相邻的切点时,芯模转角用θ表示。
导丝头往返一次,即出现起始切点时序相邻的切点时芯模转角用θn表示。
导丝头走一个单线程,即单程线缠绕,芯模转角用θt表示。则

(ⅱ)二切点线型。二切点线型也属于多切点线型,所谓多切点线型是指与起始切点相邻的切点在时序上并不相邻,即对应起始切点出现第一个位置相邻的切点时,封头极孔上已有几个切点——初始切点。这种缠绕规律统称为多切点线型。根据初始条件的不同,多切点线型又分为二切点、三切点……n切点线型。对于二切点线型来说它是指与起始切点位置相邻的切点在时序上与起始切点位置相邻的切点在时序上与起始切点间隔一个切点,即构成两切点线型。二切点线型图如图7-10。


(ⅱ)二切点线型。二切点线型也属于多切点线型,所谓多切点线型是指与起始切点相邻的切点在时序上并不相邻,即对应起始切点出现第一个位置相邻的切点时,封头极孔上已有几个切点——初始切点。这种缠绕规律统称为多切点线型。根据初始条件的不同,多切点线型又分为二切点、三切点……n切点线型。对于二切点线型来说它是指与起始切点位置相邻的切点在时序上与起始切点位置相邻的切点在时序上与起始切点间隔一个切点,即构成两切点线型。二切点线型图如图7-10。

因为在两切点的线型中,从起始切点1开始缠绕,芯模转过360°/2时,纤维缠绕到切点2的位置,芯模再转过360°/2时,纤维才缠到与切点1位置相邻的切点3,并错过了一个微量Δθ,所以Δθ是转过了两个360°/2后错过的,因此每转过一个360°/2时就错过了Δθ/2。
(ⅲ)三切点线型。所谓三切点线型是指起始切点位置相邻的切点,在时序上与起始切点间隔两个切点、构成了三切点线型。三切点线型如图7-11所示。
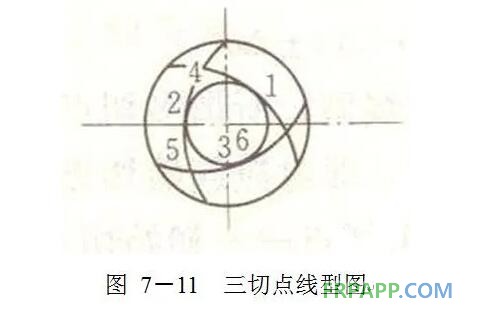
从图中可以看出,与起始切点1位置相邻的切点4,在时序上和切点1间隔两个切点——即切点2和切点3;同样道理,与切点2位置相邻的切点5在时序上与切点2间隔两个切点——切点3和切点4;与切点3位置相邻的切点6,在时序上与切点3间隔两个切点——切点4和切点5。所以三切点的线型在极孔圆周被3个初始切点等分。因此,纤维由起始切点缠到时序相邻的切点2时,芯模至少要转过360°/3,或者再加上360°的整数倍N,考虑到纤维的错位还应引入微量Δθ1,所以三切点线型的缠绕规律为:


从图中可以看出,与起始切点1位置相邻的切点4,在时序上和切点1间隔两个切点——即切点2和切点3;同样道理,与切点2位置相邻的切点5在时序上与切点2间隔两个切点——切点3和切点4;与切点3位置相邻的切点6,在时序上与切点3间隔两个切点——切点4和切点5。所以三切点的线型在极孔圆周被3个初始切点等分。因此,纤维由起始切点缠到时序相邻的切点2时,芯模至少要转过360°/3,或者再加上360°的整数倍N,考虑到纤维的错位还应引入微量Δθ1,所以三切点线型的缠绕规律为:

式中θn表示在极孔圆周上由切点n开始,缠绕到时序相邻的切点(n+1)时,芯模转过的中心角。
缠绕用导丝头每经过极孔一次,纤维在极孔上有一个切点,所用θn也表示,导丝头每往返一次,芯模转过的中心角。因此,上式是用“切点法”分析缠绕规律的基本数学表达式。但此方法也有不妥善之处。在前面的讨论中,我们实际上假定初始切点出现的顺序为依次出现,对它们的排列顺序没有分析。在实际缠绕工艺中,除了单切点线型和双切点线型不存在初始切点排列外,三切点以上的线型还存在一个初始切点的排列顺序问题。
公式中n表示线型的切点数,即极孔圆周上出现第一个与起始位置相邻的切点前,所有时序相邻切点数目。(n为1、2、3……)。N表示由初始切点n缠绕到切点(n+1)时,芯模转过360°的整数倍,是包括零的正整数,即0、1、2……。
当n≥3时,即三切点以上的线型,在与初始切点位置相邻切点出现之前,在极孔圆周上有3个以上的初始切点,这就存在一个初始切点先后的排列顺序问题。
如前所述,三切点有两种排列顺序,四切点有2种排列顺序,而五切点有4种排列顺序。因此,三切点线型有:


圆周排列顺序不同,或者说是导丝头往返运动一次时,芯模必须转过的中心角规律的不同。其中K值为正整数,K=1、2、3……n-1。K值要求应使K/n为最简真分数。
综上所述,在一个完整循环中,切点数不同,则纤维排布顺序和花纹特征(交叉点数、交带、节点数等)不同,即线型不同,导丝头往返一次芯模转角不同;如果在一个完整循环中,切点数相同而切点排布顺序不同,则纤维排布特征(线型)也不同,导丝头往返一次的芯模转角也不同。也就是说导丝头往返一次的芯模转角与缠绕线型有着严格的对应关系。因此,我们导丝头往返一次的芯模转角


(2)转速比与线型的关系。线型与速比均属缠绕规律问题,线型是指纤维在芯模表面的排布规律,而转速比是指芯模与导丝头相对运动的规律。它们是完全不同的两个概念。但是正如前面所述,不同的线型严格对应着不同的转速比。所以我们定义线型在数值上等于转速比,也就是说,速比的数值作为线型的“代号”,即:
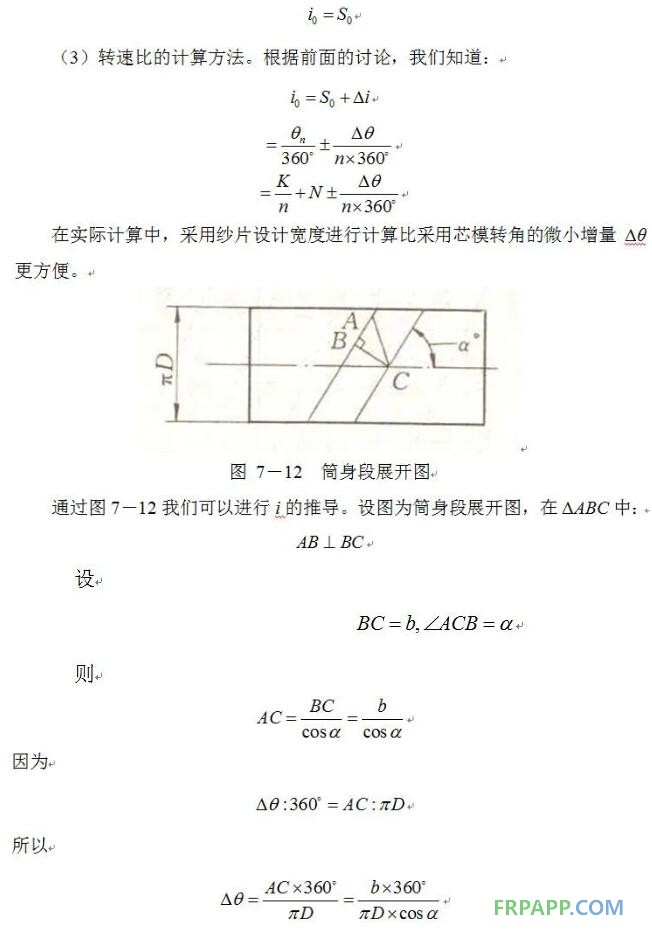



(2)转速比与线型的关系。线型与速比均属缠绕规律问题,线型是指纤维在芯模表面的排布规律,而转速比是指芯模与导丝头相对运动的规律。它们是完全不同的两个概念。但是正如前面所述,不同的线型严格对应着不同的转速比。所以我们定义线型在数值上等于转速比,也就是说,速比的数值作为线型的“代号”,即:


工艺上为避免纤维滑线,通常取负值。而实际计算时,i取至小数点4~6位。
C.线型设计
(1)稳定缠绕芯模转角的计算。对于一个具体制件来说,在原始的几何尺寸,容器工作压力及极孔等给定的条件下,如何从缠绕工艺出发,实现产品的成型呢?这就要求缠绕过程中,如何选定芯模的转角θn,因为它对应着固定的线型和转速比。
我们已经知道,不同的n、N、K对应着不同的θn,也就是说满足纤维有规律均匀布满芯模表面两条件的芯模转角θn有若干个。但对于一个确定产品,并非所有的θn都合适。如果按表7-1中任选一个θn,并考虑到速比微调±Δθn进行缠绕,尽管也满足了均匀布满的两个条件,但未必就能达到均匀布满的目的。因为纤维在容器表面及封头曲面上的位置不一定稳定,有可能出现纤维滑线的现象。从理论上讲,封头不滑线的必要条件就是使纤维位于封头曲面上的测地线上,于是,便产生了纤维缠绕能有规律地均匀布满芯模表面的第三个条件——纤维位置稳定的条件,这要求缠绕在芯模表面上的每束纤维都是其相应曲面的测地线。下面,讨论有封头的圆筒形容器的测地线的确定的问题。
在筒身段任意缠绕角的螺旋线都是测地线;在封头处缠绕则要求

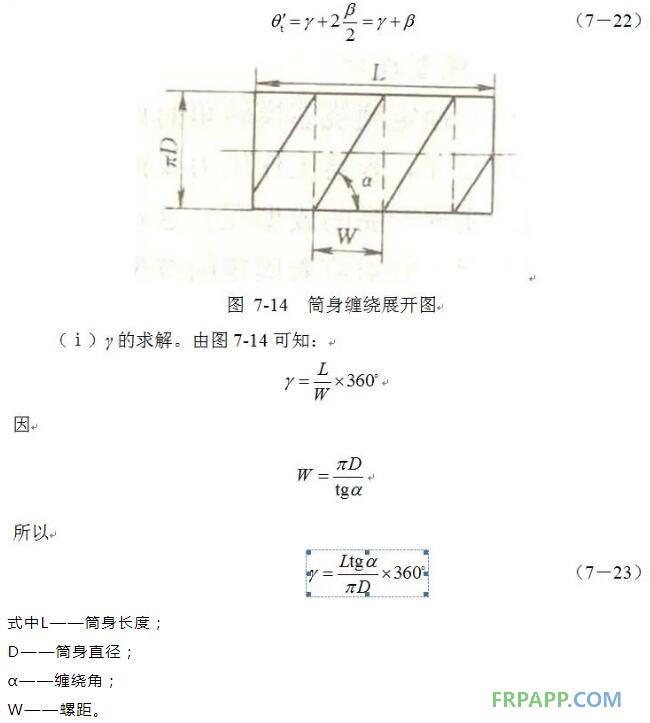
(ii)β的求解。对于封头曲面测地线缠绕所对应的芯模转角的计算比较复杂。并且目前缠绕轨迹是近似于测地线的平面曲线。所以我们通常采用平面假设法对封头部分芯模转角进行计算。
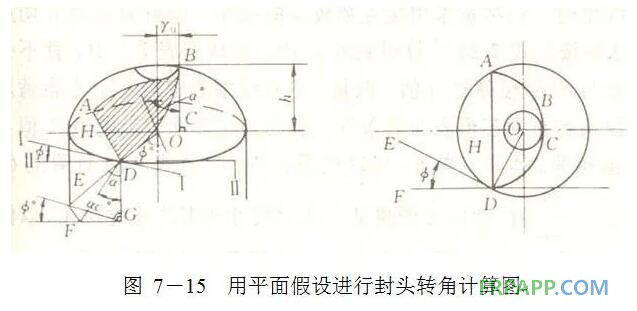
如图7-15所示,过纤维在赤道圆的两个交点(A、D)作一平面与极孔圆相切(切点为β),与封头曲面相截的交线(平面曲线ABC)即为纤维缠绕轨迹。此平面称为截平面,与筒体轴线夹角为α0,封头缠绕芯模的转角为

过D点作平面II平行平面BHC,与截平面的交线为DF。过D点作筒体的切平面I与截平面的交线为DE。平面I与II的交线为DG,过G点作平面与DG垂直,与平面I和II相交的交线分别为EG和FG,与截平面交线为EF。



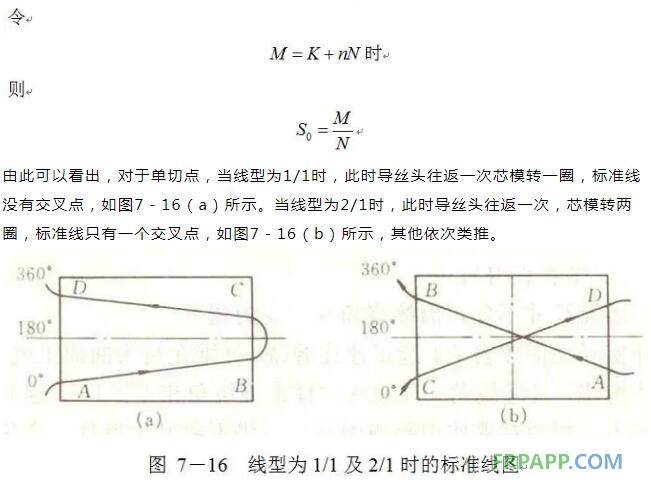
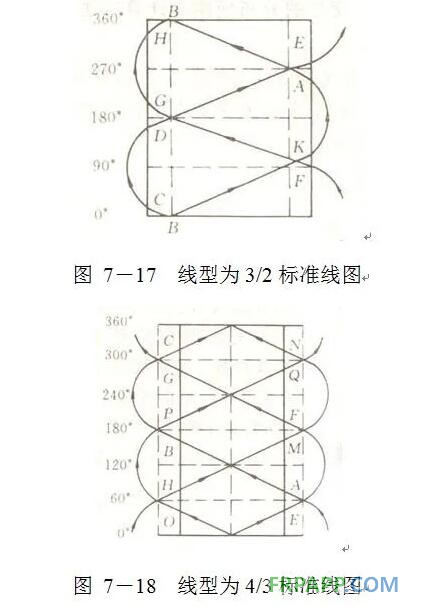
由此可知,缠绕完标准线时,交叉点数与芯模转数M有关。对于单切点线型,交叉点数等于芯模转数减1,即xn-1=M-1。对于多切点线型,缠绕完标准线,导丝头要往返多次、这样相交的次数就与导丝头往返次数(切点数)有关。例如,线型为3/2时,缠绕完标准线,芯模转3圈,导丝头往返2次,交叉点共有4个,即交叉点数等于芯模转数减1的2倍,即xn-2=2(M-1),如图7-17所示。当线型为4/3时,缠绕完标准线,芯模转4圈,导丝头往返3次,共有9个交叉点,即交叉点数等于芯模转数减1的3倍,即xn-3=3(M-1),如图7-18所示。其余以此类推,对于n切点线型,交叉点数等于芯模转数减1乘切点数,xn=n(M-1)。


(ii)β的求解。对于封头曲面测地线缠绕所对应的芯模转角的计算比较复杂。并且目前缠绕轨迹是近似于测地线的平面曲线。所以我们通常采用平面假设法对封头部分芯模转角进行计算。

如图7-15所示,过纤维在赤道圆的两个交点(A、D)作一平面与极孔圆相切(切点为β),与封头曲面相截的交线(平面曲线ABC)即为纤维缠绕轨迹。此平面称为截平面,与筒体轴线夹角为α0,封头缠绕芯模的转角为

过D点作平面II平行平面BHC,与截平面的交线为DF。过D点作筒体的切平面I与截平面的交线为DE。平面I与II的交线为DG,过G点作平面与DG垂直,与平面I和II相交的交线分别为EG和FG,与截平面交线为EF。




由此可知,缠绕完标准线时,交叉点数与芯模转数M有关。对于单切点线型,交叉点数等于芯模转数减1,即xn-1=M-1。对于多切点线型,缠绕完标准线,导丝头要往返多次、这样相交的次数就与导丝头往返次数(切点数)有关。例如,线型为3/2时,缠绕完标准线,芯模转3圈,导丝头往返2次,交叉点共有4个,即交叉点数等于芯模转数减1的2倍,即xn-2=2(M-1),如图7-17所示。当线型为4/3时,缠绕完标准线,芯模转4圈,导丝头往返3次,共有9个交叉点,即交叉点数等于芯模转数减1的3倍,即xn-3=3(M-1),如图7-18所示。其余以此类推,对于n切点线型,交叉点数等于芯模转数减1乘切点数,xn=n(M-1)。

由于每股纤维都对应极孔圆周上一个切点,所以在交带截圆上的交叉点数等于切点数,故交带数为yn= M-1。
由此得出结论,无论什么样的线型,交带数均为线型中分子数(即缠绕完一个完整循环的芯模转数)减1。交叉点数均为交带数与切点数的乘积。
(ii)交叉点及交带的分布规律 从纤维的连续性可知,每股纤维都对应极孔圆周上的一个切点。同时缠绕完标准线的切点等分极孔圆周。所以交带截圆上的交叉点等分该截面,即在交带截圆上两相邻交叉点间的芯模转角为360°/n。


三、缠绕规律的设计
前面已经分别用标准线法、切点法逐一分析了缠绕规律。下面就实际生产中,如何选择、设计进行讨论。
1. 选择缠绕规律的要求
(1)缠绕角α要求与测地线缠绕角相近,为更好的发挥玻璃纤维的强度,缠绕角α应近于55°。
(2)为避免极孔附近纤维的架空,影响头部强度,所选缠绕规律在封头极孔处的相交次数不宜过多。
(3)头部包角β,应接近于180°为好,一般选用β=160°~180°之间,否则会使纤维在头部引起打滑。
2. 选择缠绕规律的步骤
(1)一般情况下,把筒身圆周分为4等分,即取n=4,若分别取K=1、2、3、4、5,则缠绕规律便有5种类型:
n=4,K=1;
n=4,K=2;
n=4,K=3;
n=4,K=4;
n=5,K=1;


3. 确定缠绕规律及其他
(1)经以上计算,将上述5种线型算出的相应缠绕参数列表。再按照缠绕规律的3个选择原则,结合实际工作经验进行分析比较,经筛选后,可以得到一个比较合理的缠绕规律,这就是此产品的真正缠绕线型。
(2)根据求出的速比i值,再考虑缠绕过程中必须的错纱,为缠绕机的设计提供依据。
4. 举例
要缠制一内压容器,直径D=770mm,筒身段长L=2930mm,封头极孔直径d=385mm,封头高h=285mm,试选定缠绕线型和转速比,并画出标准线展开图。设定纱片宽b=5mm。
设计思路如下:
首先计算出按照测地线轨迹缠绕纤维,导丝头往返一次(即出现与起始切点时序相邻切点)时的芯模转角θn。按照这个速比缠绕时,可以保证缠绕到芯模表面的纤维不滑线(稳定)。但还没有满足有规律均匀布满芯模表面的条件,而满足这个条件的线型应为
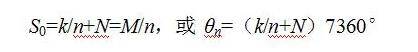
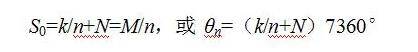
按此式计算得到的线型表中的芯模转角都可满足均匀布满的要求。但对某一具体产品来说,并不是线型表中的全部芯模转角值都能满足纤维位置稳定条件。怎样解决这个矛盾呢?首先求出测地线轨迹的芯模转角,然后再在线型表7-1中找一个与此值接近的值作为计算数据。然后调整容器的尺寸。用这个速比进行缠绕,既能满足均匀布满的条件,又能满足纤维位置稳定的条件。
那么测地线缠绕角如何求得呢?我们知道,对筒身段来说,任何角度的螺旋线都是测地线,亦即都是稳定的(实际上不必考虑纤维在筒身缠绕的稳定问题)。矛盾集中在封头曲面上,而封头曲面上的测地线方程为



















 鲁ICP备2021047099号
鲁ICP备2021047099号