雷达天线罩被强台风吹坏,经分析是由于结构原缺陷或损伤区扩大(包括结构材料和接头),接头进一步松动改变了单元件的边界条件,使单元件的应力状态恶化,反过来使接头处受力增加,接头更松动或损伤,进一步促进单元件应力状态更严重,甚至从一种应力状态突变到另一种应力状态,也即为局部失稳,或某单元件局部失稳,进一步使周围接头应力增大,逐步扩大失稳区,直到整个球壳破坏。有一个从缺陷→接头→局部失稳直到整体破坏的过程。这些缺陷有原始的,也有经老化疲劳和蠕变新增加或者是原始缺陷扩大的。另一方面,接头还有一个因工艺因素和安装因素产生的缺陷和不均匀,经过老化疲劳和蠕变后进一步扩大和恶化,从而改变雷达罩单元件或某局部区域的边界条件,促使和加快局部失稳过程。一个单元件的局部破坏,在连续的强台风的条件,必将引起罩子的整体破坏。
1 稳定概念
一根压杆从单纯受压的应力状态变成弯曲应力状态,即称为失稳,这是著名的欧拉失稳。对于一块
板,同样由受面内压缩应力状态受弯曲时,也称为失稳,只是板是四边支撑的,板的失稳临界载荷要比压杆大许多,况且,随着边界从简支心为固支,其临界载荷成倍或几十倍地增加。夹层结构因大大提高弯曲刚度,从几十倍到几百倍,因而采用夹层结构大大提高板的临界载荷。有曲率的壳体比平板不易失稳,曲率半径越小越不易换稳,当曲率半径增大时,就易失稳,直到曲率半径为∞时也即成为平板时,相对壳而言,失稳临界载荷大大降低。
压杆失稳后就不能继续承载了,但板不同,失稳后能继续承载。传统的均质的金属薄板,特别是对重量要求很严格的飞机结构,允许板失稳,对于玻璃钢复合材料,此观点同样适用。对于平板失稳,玻璃钢/复合材料不同于均质金属材料,有个最优设计的问题,对于加筋板更是允许板失稳,不仅航空上允许,对于舰船也是允许的。
对于壳体,特别是薄壳,尤其是对称旋转的薄壳,所谓失稳,事实上往往因制造缺陷等各因素,是从局部地区先失稳。对于这种薄壳,失稳后就失去实际承载的能力,也因此称为整体失稳。对于对称性薄壳,又在对称边界条件,往往以整体失稳的临界载荷作为设计指标。
夹层结构板或壳的失稳又有一些新的内容:①即使对于夹层结构压杆,除必须计及芯子剪切变形影响的修正欧拉压杆临界载荷外,还有剪切失稳,面板局部失稳;②对于夹层结构板,除计及剪切变形的临界载荷外,其中特别重要的有面板象支持弹性基础上的局部皱曲失稳,对于蜂窝芯子这类孔状芯子,又有孔内面板局部失稳;③对于夹层结构壳,在对称载荷及旋转壳的情况下,与夹层结构板差不多,有面板局部失稳临界载荷。对于非对称载荷旋转壳、对称载荷非旋转壳、非对称载荷非旋转壳的这类壳体,还应有一个它们特有的局部失稳,在此方面极少见到成熟的理论和计算公式。可应用微分几何和差方原理进行分析计算。由于复杂性,还没有像上述那些板壳有计算公式。目前只能用特殊处理过的有限元数值计算。
2 破坏现象
从几只雷达罩破坏现象可以看出,面板、芯子有发白、分层,接头螺孔变形很大,孔边发白、分层等,螺栓弯曲,单元件凹陷、折断等。这是一个原材料质量欠佳或不均匀→工艺缺陷及不均匀→接头安装不到位及不均匀→老化→疲劳→蠕变→局部损伤→接头松动损伤→局部失稳。整体破坏的过程。对有关问题在有关“工艺”“接头”两文叙述。
从破坏现象可知,对于上述的几种失稳,还要增加:①缺陷、分层对失稳临界载荷的影响;②接头松动或局部损伤,即边界缺陷对失稳临界载荷的影响;③当①、②共同存在时,对失稳临界载荷的影响。
3 球壳稳定性
均匀球壳在均匀外压下的稳定性早在1915年已得出,对金属材料,泊松比为0.25,稳定k系数为1.193,是很大的,不少研究者对其进行理论和实验的研究,k逐步从0.5~0.6直到0.25~0.3。对于各向异性的玻璃钢/复合材料,k取0.18~0.25,一般取0.2,这是从钢结构球壳的经验k系数推导出来。对于夹层结构球壳,其厚度和弹性模量是从夹层结构球壳与单层均质球壳的等拉伸刚度和等弯曲刚度的条件推导的折算厚度和弹性模量。
当单层球壳k系数取0. 2,肯定是偏于安全的。球壳经风洞试验,当k取0.3时,球壳还未破坏,况且风洞的风速是向一个方向吹来,要比均匀外压严重。但是对于夹层球壳,稳定计算必须涉及芯子剪切变形的影响。也足以说明芯子剪切变形对曲板临界载荷的影响。对复合材料,特别是夹层结构的壳体,复合材料分层,面板与芯子脱胶失稳,均对临界载荷有影响。
4 雷达天线罩稳定性
玻璃钢夹层结构雷达天线罩的稳定性,除具有球壳稳定性的共性外,还有其特性。这当中,有二个特性必须强调:①由于罩子是许多分块构成,同时强台风本身强度很不均匀,同时又是从一个方向或几个方向吹向罩子,一定存在一个以单元体为中心的局部稳定性问题。根据罩子半径和厚度,以及接头的布置及质量,以及风力强度和分布,有一个以一块单元局部失稳和一个以几块单元体的局部失稳;②面板本身的局部失稳。
4.1 罩子局部失稳
理论上精确计算罩子的局部稳定性,是极其困难和复杂的。目前还没有可供应用的计算公式。我们可以根据罩子的实际受力情况,按文献[14」中的根据具体情况进行具体分析的指导思想,该文献是针对变曲率壳体在均匀外压下的稳定性提出的采用一个加权曲率半径的方法。
对于我们均匀的球壳,在有分块,且外载荷极不均匀的情况下,我们可以采用如下方法。先用通常载荷计算出罩子的无矩理论的面内应力,这应力是不均匀的,然后取一块面应力最大的单元件,用加权的方法计算出这块单元件当作承受均匀面应力的应力值。这块单元件通过接头弹性支撑在罩子的其它单元件上。为了说明此块单元件的局部稳定性间题,可以暂时假设单元件边界是简支。这块单元件是在最强的台风速的压力作用下,因此这块单元件则成为在压弯受力的单元体。
如按无矩理论计算出单元体面内正应加σx、αy、τxy对于矩形单元体,可以以球体的经纬线方向定为x,y方向)。然后计算出临界应力σxcr、σycr、τcr、σxcr、σycr。用文献[6]中的式(2.5〕表6.1~6.10,τcr用表6.11~6.21,再计算出单元体单承受横向分布载荷下的破坏载荷qB。
则可以按下式核算罩子单元件的强度:
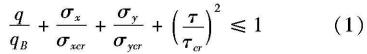
这实际上是这单元件在局部最强的风压力9作用下,其曲率越来越小,直到曲率为零,即曲率半径为∞,这时,在σx、σy、τxy作用下突然失稳,直接影响周围其它单元件,而发生最后破坏。
4.2 面板局部皱曲失稳
对于夹层结构,具有特有面板类似于支持在芯子弹性基础上的局部皱曲失稳,其计算公式为:
其中,k’为稳定系数,是与成型工艺、面板初曲率、面板与芯子胶接强度及几何尺寸等有关的常数,k’的范围为0.05~0.32。
另外,还有芯子剪切失稳,计算公式为:
除非面板较薄,并且蜂格较大,才会出现蜂格由酒窝型(凹陷)局部失稳,如文献[7]中的式(3.2)。
5 实际使用中的稳定性
雷达天线罩经几年使用后,经过大气自然老化,反复受强风的疲劳,及长期自重及风载作用的蠕变,使夹层结构材料在刚度和强度方面均退化,具体来讲,面板拉压、剪切强度下降,面板Ef及芯子的Gc、Ec下降,使式(1)中的qB,σxcr、σycr、τcr减小,这样就容易在特别大的台风作用下,在受力最大的单元体首先局部失稳破坏。
另外,Ef、Ec、Gc下降,特别式(2)中k’系数也下降,这样也会使面板发生局部皱曲失稳,经过长期使用后,会出现面板局部皱曲或剪切失稳。面板局部失稳又会影响单元件的受力状态,使单元件的受力更严重,促使单元件失稳。
另外,接头经过长期使用后,会松动,甚至于出伤,这样也可使式(1)的qB,σxcr、σycr、τcr减小,从而加剧单元体失稳。
6 结束语
雷达天线罩是一个完整的产品,目前设计水平还未达到安全系数设计一致,在设计过程中必须有存在安全系数较小的部位。一个产品正象一只木桶,木桶的各块木条是一样的长短,当某木条短后,这木桶的水就要流出,只能达到短木条的水平,因此必须对产品的各个部件、部位,各种应力状态,进行精细准确的设计,使各部位、各种受力状态达到同样安全可靠程度。
另外,产品设计必须涉及老化、疲劳、蠕变等因素,不能只靠提高安全系数来解决,应从实际试验数据出发。目前还没有数据,可参考国内外有关资料。研究所及设计部门应加强这方面的基础研究工作,以便提高产品设计水平,确保产品长期使用质量。
对上述提出一些罩子特有的局部稳定性,要深入研究。
对于材料缺陷及接头松动,退化等对产品稳定却影响,也要加强研究。
必须尽快到破坏罩子现场取样,全面进行试验,取得第一手最宝贵资料。
经过试验,分析,理论计算,将会变坏事成好事。
通过这一次分析研究,必须加强产品的原材料、生产工艺过程、出厂、安装的检验,并制定有关标准规范,并规定各岗位的责任制。














 鲁ICP备2021047099号
鲁ICP备2021047099号