复合材料壳体FEA中的材料工程特性参数转换

      在对结构进行有限元分析时，结构材料的工程常数是一组非常重要的特性参数。必须确保程序输入的材料的工程常数的准确性，才能保证有限元分析结果的正确性和有效性。对于简单的各向同性材料，可看作每一个平面都是对称面，每一个方向都是弹性对称轴，也即其体内每一点的任意方向上的弹性性质都相同。因此，对于各向同性材料，弹性常数对任意正交坐标系是不变的。而各向异性材料最突出的特点，就是它的方向性，各向异性材料的弹性系数是方向的函数，它们和坐标的取向有关。

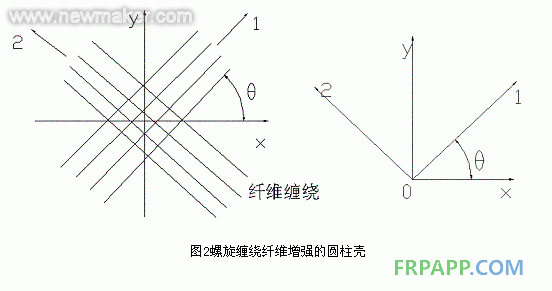
       在利用ANSYS有限元程序对纤维增强复合材料气瓶进行应力分析时，遇到了如何正确确定复合材料弹性常数的问题。因为多层复合材料缠绕结构中，不同的缠绕层有不同的缠绕方向，也就是不同的纤维缠绕层有不同的材料坐标系。而复合材料与均质各向同性材料的主要本质差别在于：即使在宏观上看，也会呈现出明显的非均质各向异性，尤其纤维增强复合材料的各向异性特性显得更加强烈。即纤维增强复合材料在不同的坐标方向上有不同的弹性特性。

       通过材料实验所得到的是材料主轴坐标方向上的弹性系数值，而利用ANSYS进行有限元分析时，程序要求输入的是与系统整体的求解坐标系相一致的弹性参数。因此，对于有着不同缠绕方向的多层复合材料来说，存在将弹性系数由材料主轴坐标系向系统整体坐标系进行转换的问题。这种转换并不是实际物理意义上的转换，而是一种为简化分析过程的等效参数转换，因此其正确性需要实际计算的验证。

      利用ANSYS的结构非线性分析功能，对一复合材料缠绕壳体进行应力分析。壳体模型为一六层结构，最内层为铝内胆层，外层为连续五层的复合材料缠绕层，前三层为碳纤维缠绕层，缠绕方向分别为环缠、螺旋缠和高角缠绕；后两层为玻纤缠绕层，缠绕方向分别为螺旋缠绕和环向缠绕。由于壳体的对称性结构，因此选用ANSYS的轴对称单元对其进行分析。壳体施加内压载荷作用。

       计算出不同缠绕方向材料坐标系上的工程常数转换到统一的整体坐标系上的等效的工程常数，然后按不同层分别输入不同的工程常数值，利用ANSYS的非线性功能分别在不同内压载荷作用下进行求解，最后得到各个层的应力值分布。

       由图可以看出，每个单层内部的应力水平接近，而不同层间的应力具有不同的应力水平；这种应力的分布规律也是符合纤维的不同缠绕方向的。用ANSYS分析的结果和与实验所得结果进行比较，其吻合程度较好。因此，这就充分证明，对于材料主轴方向不一致的各向异性材料组成的这种层状结构，利用坐标变换的方法对其工程常数进行等效变换是可行的