复合材料风电叶片有限元刚度分析

 引言

复合材料叶片是风机设备中将风能转化为机械能的关键部件[1]。目前，叶片尺寸正在朝着大型化的方向发展，而其结构性能试验的成本也随之增加，因此，找到一种有效的结构计算分析方法对于节约成本以及结构校核和开发新型叶片就显得尤为重要。

随着计算机技术的发展，有限元法在结构分析中得到了广泛的应用。有限元强大的建模和结构分析功能适用于复合材料叶片的应力、变形、频率、屈曲、疲劳及叶根强度分析。ANSYS是一款著名的商业化大型通用有限元软件，广泛应用于航空航天、机械制造等领域。ANSYS多物理场仿真及耦合的独特功能，以及200多种单元类型，可以对复合材料结构设计、材料研究及制造工艺提供完整的解决方案。总之，对于复合材料结构计算分析，完全可以通过ANSYS程序来实现[2]。

但是，因复合材料叶片结构的特殊性，例如：①形状不规则（每个截面都不同）；②铺层复杂，过渡层很多；③大量夹层结构（“三明治”结构）；④大量粘结区域。所以，其有限元模型的建立是叶片结构有限元分析中的一大难题，而单元类型的选择又决定着建立有限元模型的难易。目前，复合材料风电叶片有限元模型在单元类型的选择上主要采用三种单元类型：shell99壳单元、shell91壳单元、Solid46实体单元。选择实体单元，虽然能提高有限元的计算精度，但是建立叶片的有限元模型会花费大量的工作时间，且很难定义单元坐标，这非常不利于工程上叶片的结构校核及分析；选择壳单元，可以方便地设置和修改铺层厚度，单元坐标的设置容易实现，建模和计算时间比采用实体单元少，这极大地提高了工作效率，而且其计算精度完全可以满足工程需要。

因此，本文使用shell99壳单元，通过三维建模，建立了叶片的有限元模型，并以悬臂梁的方式，对叶片的模态和静力变形进行了计算分析，通过计算，得出了叶片的重量、振型及最大变形，并与试验数据进行了对比。 

1 有限元模型的建立

通常，在整个有限元求解过程中最重要的环节是有限元前处理模型的建立。一般包括几何建模、定义材料属性和实常数（要根据单元的几何特性来设置，有些单元没有实常数）、定义单元类型，网格划分、添加约束与载荷等。

由于叶片形状复杂，而一般有限元软件所提供的几何建模工具功能相当有限，所以在ANSYS中难以快速方便地对其建模。因此，针对较复杂的结构，可以先在三维CAD软件（如在PROE中）建立几何模型，然后在有限元分析软件ANSYS中通过输入接口读入实体模型，最后，在ANSYS环境下，通过几何修补和简化、板壳中面抽取、节点偏置、网格自动划分等技术对叶片模型进行处理，并形成高效准确的有限元模型，使之适用于CAE分析。

1.1 单元设置与材料属性

针对叶片中的梁、壳等复合材料层合结构，ANSYS提供了一系列的特殊单元——结构多层复合材料单元，以模拟各种复合材料。铺层单元中可以考虑复合材料特有的铺层特性和各向异性特性。

本计算采用的是相对简单的线性铺层单元Shell99。该单元是一种八节点3D壳单元，每个节点有六个自由度，主要适用于薄到中等厚度的板和壳结构，一般要求宽厚比应大于10。Shell99可实现多达250层的等厚材料层，或者125层厚度在单元面内呈现双线性变化的不等厚材料层。如果材料层大于250，用户可通过输入自己的材料矩阵形式来建立模型，还可以通过一个选项将单元节点偏置到结构的表层或底层。

单元铺层主要是确定纤维方向和纤维量，是复合材料风电叶片结构设计的一个重要环节。铺层设计的优劣在很大程度上决定着结构设计的成败[3]。

本计算的铺层完全按照工艺铺层进行设计。在ANSYS环境下，针对Shell99单元，通常有两种方法来定义材料层的配置：①通过定义各层材料的性质；②通过定义表示宏观力、力矩与宏观应变、曲率之间相互关系的本构矩阵。第一种方法是由下到上一层一层定义材料层的配置，底层为第一层，后续的层沿单元坐标系的Z轴正方向自底向上叠加，对于每一层材料，由单元实常数表来定义材料性质、铺层方向角、厚度，如图1所示为叶片某部分的单元铺层；第二种方法是定义各层材料性质的另一种方式，矩阵表示了单元的力-力矩与应变-曲率的关系，必须在ANSYS外进行计算。

 

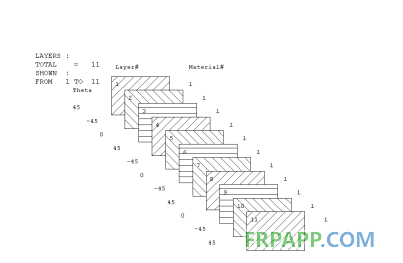
图1.单元铺层图

Fig.1 element laminated diagram

叶片的材料体系为玻纤/环氧，叶片制作采用真空灌注工艺，所用复合材料有：三轴向玻璃布、双轴向玻璃布、单轴向玻璃布、PVC泡沫、Balsa木、毡等。玻璃钢复合材料与泡沫材料的主要力学性能见表1、表2所示，其中，Ex为材料的纤维方向，玻璃钢复合材料的密度取ρ=1888kg/m3，Balsa木密度取ρ=150kg/m3，PVC密度取ρ=80kg/m3。

表1.玻璃钢复合材料力学性能

Table 1. Mechanical properties of FRP materials

名称	符号	单位	UD	Biaxial	Triaxial
玻纤/环氧	Ex	Mpa	39000	11400	28500
	Ey	Mpa	8920	11400	13500
	Ez	Mpa	8920	8920	8920

表2.泡沫材料力学性能

Table 2. Mechanical properties of foam materials

名称	符号	单位	模量值
Balsa木	Ex	Mpa	1000
	Ey	Mpa	35
PVC	Ex	Mpa	65

1.2 模型建立与网格划分

首先，依据三维坐标变换原理求解出叶片空间截面翼型的实际位置，然后以大型三维软件PROE为工作平台，通过导入空间坐标点，生成B样条曲线，如图2所示为本计算模型的三维线框图。

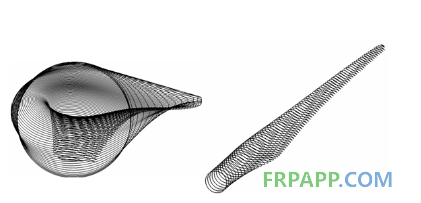
图2.叶片线框投影图

Fig.2 Blade frame drawing

　　最后，由曲面扫掠命令生成叶片三维外形图，再结合曲面曲线分析命令对所生成的曲线、曲面进行检验和修改，直至生成符合要求的叶片三维外形图，如图3所示。将生成的三维模型转化为IGES格式文件，为后续建立有限元模型做准备。

 

图3.叶片外形图

Fig.3 Blade outline diagram

将PROE导出的IGES格式文件，输入到ANSYS系统中，得到了ANSYS环境下的叶片三维模型。采用Shell99单元对叶片壳体、梁、腹板进行网格划分，有限元模型单元数为29914，节点数为88680，如图4所示。

 

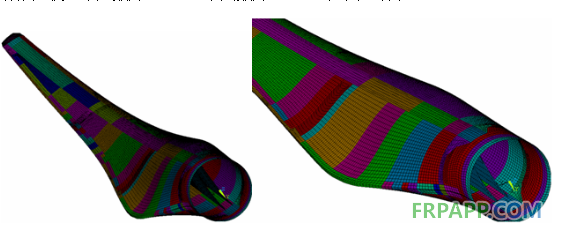
图4.网格划分图

Fig.4 Meshing diagram

1.3 约束与载荷

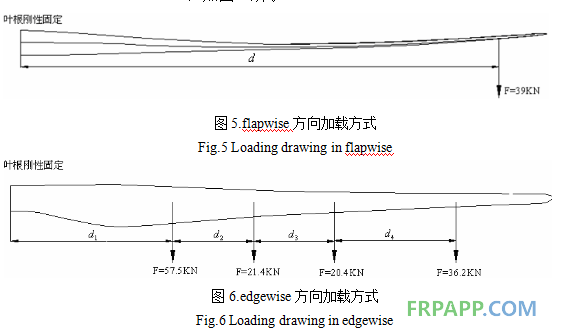
叶片根部采用刚性固定的约束形式，即根部所在节点的6个自由度被固定，整个叶片简化为悬臂梁模型。加载方式与试验加载方法保持一致，第一个工况，即在flapwise方向，选择单点加载，施加集中力39KN，如图5所示；第二个工况，即在edgewise方向，选择四点加载，从左至右分别施加集中力57.5KN、21.4KN、20.4KN、36.2KN，如图6所示。

 

2 计算结果与分析

2.1 质量计算结果

表3即为ANSYS输出的风电叶片质量计算结果，重心位置与实测值基本吻合，叶片总质量低于实际值。产生叶片质量计算值比实测值小的主要原因是叶片灌胶后，其泡沫的密度应该大于实际泡沫的密度，以及建立的叶片有限元模型没有考虑实际叶片中的附件（如接闪器等金属件）重量等。

表3.风电叶片质量计算结果

Table 3. The mass result of the blade

	质量[kg]	重心（距叶根）[m]
实际值	5950	12.1
有限元计算值	5571	11.9
误差	6.4%	1.65%

2.2 模态分析结果

表4即为ANSYS输出的风电叶片一阶固有频率计算结果，并且提取了叶片的前五阶振型，如图7所示。

表4.风电叶片一阶固有频率计算结果

Table 4. The first natural frequency of the blade

	频率值[Hz]
	一阶flapwise方向	一阶edgewise方向
试验值	0.8	1.46
计算值	0.89	1.61
误差	11.25%	10.27%

由图7可知，一阶频率为flapwise方向一阶固有频率，二阶频率为edgewise方向一阶固有频率。由表4知叶片一阶固有频率的计算值比实测值大，造成计算值偏大的主要原因是叶根约束方式与试验（通过螺栓固定）不一致，以及计算质量小于实际质量等。

 

图7.振型图

Fig.7 Vibration mode diagram

2.3 静力分析结果

　　表5即为两种工况下计算出的风电叶片最大挠度值，计算结果与实测值吻合较好。

表５.两种载荷工况下风电叶片的最大挠度

Table 5. The most displacement of the blade in the two load case

	叶片最大挠度[m]
	flapwise方向	edgewise方向
试验值	5.36	1.11
计算值	4.83	1.01
误差	9.9%	9%

叶片变形如图8、图9所示。

 

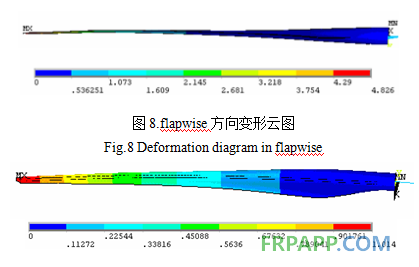
图9.edgewise方向变形图

Fig.9 Deformation diagram in edgewise

3 结论

(1) 采用壳单元模拟风电叶片计算出叶片总质量、挠度变形能与实测结果相对误差小于10%，证明了该方法在工程应用上的可行性和可靠性。

(2) 由于叶根约束方式与试验（通过螺栓固定）不一致以及计算质量小于实际质量等原因，叶片固有频率的计算值略高于实测结果。

(3) 采用壳单元计算风电叶片刚度，既可保证计算结果的可靠性又可缩短建模时间提高工作效率，对风电叶片结构分析的实际工程应用具有重要价值。